Recursive binary tree traversal algorithm in java (preOrder /postOrder/inOrder)

2 Comments / By /
  • Given a binary tree, traverse the binary tree using recursive algorithm.
  • Binary tree traversal is categorized into two parts.
    • Depth first search traversal (recursive algorithm)
      • Pre Order Traversal
      • Post Order Traversal
      • In Order Traversal
    • Breadth First search (BFS) or Level Order Traversal (non-recursive) algorithm.
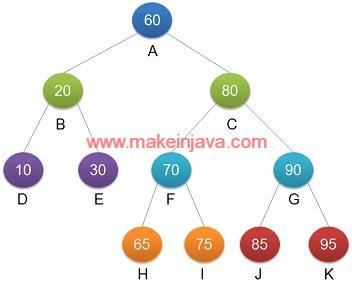
Traverse binary tree (DFS)
Fig 1: Traverse binary tree (DFS)

Applications of depth first search:

Examples of PreOrder, PostOrder & InOrder (DFS) algorithm (java).

Example 1 (PreOrder binary tree traversal):

  • In preOrder traversal:
    • We are visit current node, then
    • We visit left child node, then
    • We visit right child node.
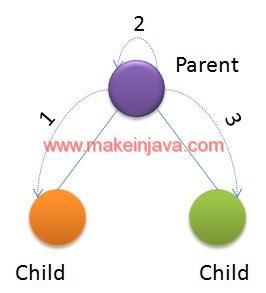
  • We have shown the preOrder traversal in Fig. 2:
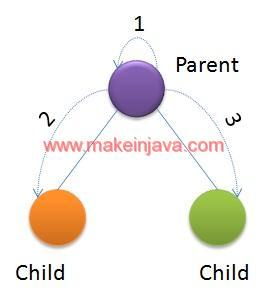
PreOrder example binary tree
Fig 2:PreOrder traversal
  1. Visit parent node or current node
  2. Visit left child
  3. Visit right child

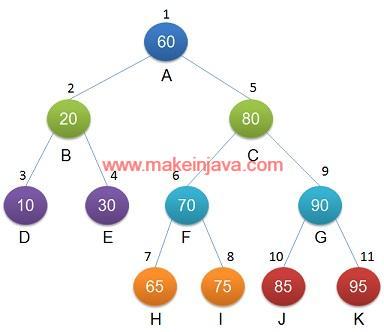
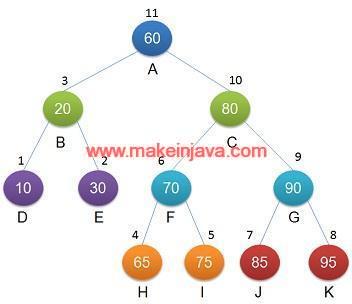
PreOrder binary tree traversal of binary tree shown in Fig 3 is:
60 20 10 30 80 70 65 75 90 85 95

PreOrder binary tree traversal
Fig 3: PreOrder traversal of binary tree
public static void preOrder(Node root) {
    if (null == root) {
        return;
    }
    System.out.printf("%d ", root.data);
    preOrder(root.left);
    preOrder(root.right);
}

Example 2 (PostOrder binary tree traversal):

  • In postOrder traversal:
    • We visit left child, then
    • We visit right child, then
    • We visits current node.
  • We have shown the postOrder traversal in Fig. 4:
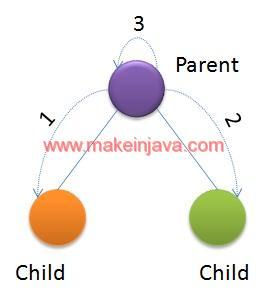
PostOrder example binary tree
Fig 4: PostOrder traversal
  1. Visit left child
  2. Visit right child
  3. Visit parent node or current node

PostOrder binary tree traversal of binary tree shown in Fig 5 is:
10 30 20 65 75 70 85 95 90 80 60

PostOrder binary tree traversal
Fig 5: PostOrder traversal of binary tree
public static void postOrder(Node root) {
    if (null == root) {
        return;
    }
    postOrder(root.left);
    postOrder(root.right);
    System.out.printf("%d ", root.data);
}

Example 3 (InOrder binary tree traversal):

  • Using InOrder traversal:
    • We first visits the left child, then
    • Current node, then
    • Right child of binary tree.
  • We have shown the inOrder traversal in Fig. 6:
InOrder example binary tree
Fig 6: InOrder example tree
  1. Visit left child
  2. Visit parent node or current node
  3. Visit right child

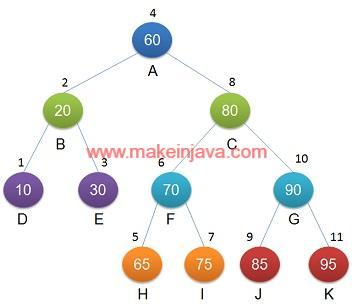
InOrder binary tree traversal of binary tree shown in Fig 7 is:
10 20 30 60 65 70 75 80 85 90 95

InOrder binary tree traversal
Fig 7: InOrder binary tree traversal
public static void inOrder(Node root) {
    if (null == root)
        return;
    inOrder(root.left);
    System.out.printf("%d ", root.data);
    inOrder(root.right);
}

Time complexity of algorithm is O(n).

Program: traverse binary tree in PreOrder, PostOrder & InOrder using java

1.) DFSTraversal Class:

DFSTraversal class performs the following operations:

  • preOrder traversal
  • postOrder traversal
  • inOrder traversal
package org.learn.Question;
 
public class DFSTraversal {
     
    public static void preOrder(Node root) {
        if (null == root) {
            return;
        }
        System.out.printf("%d ", root.data);
        preOrder(root.left);
        preOrder(root.right);
    }
     
    public static void postOrder(Node root) {
        if (null == root) {
            return;
        }
        postOrder(root.left);      
        postOrder(root.right);
        System.out.printf("%d ", root.data);
    }
     
    public static void inOrder(Node root) {
        if (null == root)
            return;
        inOrder(root.left);
        System.out.printf("%d ", root.data);
        inOrder(root.right);
    }
     
     
}

2.) Node Class:

  • Node class is represents the nodes of a binary tree.
package org.learn.Question;
 
public class Node {
    public int data;
    public Node left;
    public Node right;
 
    public Node(int num) {
        this.data = num;
        this.left = null;
        this.right = null;
    }
 
    public Node() {
        this.left = null;
        this.right = null;
    }
     
    public static Node createNode(int number) {
        return new Node(number);
    }
}

3.) App Class:

  • We are creating the binary tree in main method.
  • We are calling the method of DFSTraversal class to perform preOrder, postOrder and inOrder traversal.
package org.learn.Client;
 
import org.learn.Question.DFSTraversal;
import org.learn.Question.Node;
 
public class App {
    public static void main(String[] args) {
        // root level 0
        Node A = Node.createNode(60);
        // Level 1
        Node B = Node.createNode(20);
        Node C = Node.createNode(80);
        // Level 2
        Node D = Node.createNode(10);
        Node E = Node.createNode(30);
        Node F = Node.createNode(70);
        Node G = Node.createNode(90);
        // Level 3
        Node H = Node.createNode(65);
        Node I = Node.createNode(75);
        Node J = Node.createNode(85);
        Node K = Node.createNode(95);
 
        // connect Level 0 and 1
        A.left = B;
        A.right = C;
        // connect level 1 and level 2
        B.left = D;
        B.right = E;
        C.left = F;
        C.right = G;
        // connect level 2 and level 3
        F.left  = H;
        F.right = I;
        G.left  = J;
        G.right = K;
         
        System.out.println("PreOrder binary tree traversal :");
        DFSTraversal.preOrder(A);
         
        System.out.println("\nPostOrder binary tree traversal :");
        DFSTraversal.postOrder(A);
         
        System.out.println("\nInOrder binary tree traversal : ");
        DFSTraversal.inOrder(A);
    }
}

Output: preOrder, PostOrder & InOrder binary tree traversal using java

PreOrder binary tree traversal :
60 20 10 30 80 70 65 75 90 85 95
PostOrder binary tree traversal :
10 30 20 65 75 70 85 95 90 80 60
InOrder binary tree traversal :
10 20 30 60 65 70 75 80 85 90 95

Download Code – binary tree traversal algorithm (pre,post & inorder)

 

You may also like:

Print vertical order traversal of binary tree in java (recursive & example)

Find diameter of binary tree in java – DFS/recursive & example

Number of nodes or size of binary tree in java (DFS / examples)

Print ancestors of node in a binary tree (java/ recursive/ examples)

Print paths from root to leaf nodes in binary tree (Java/ recursive)

Convert binary tree to mirror/symmetric tree in java (recursive /example)

LCA (Lowest common ancestor) – binary tree (recursive / example)