Print vertical order traversal of binary tree in java (recursive & example)

• Given a binary tree, print binary tree in vertical order using recursive algorithm.
• Traverse binary tree vertically using depth first search (dfs) algorithm.
• The nodes, which are at same vertical distance, are said to be on same vertical path.
  • The root node is assumed to be at vertical distance of 0.
  • When, we traverse left subtree, we decrements the distance by 1.
  • When, we traverse right subtree, we increment the distance by 1.
• The application of vertical order traversal is Find a vertical order sum in a Binary Tree

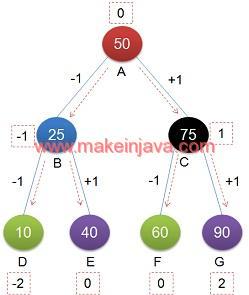
Example 1: find vertical distance of nodes in binary tree using java

• Root node A is at distance 0
• Node B is left child of node A
  • Distance of B Node is decremented  by 1.
    • Node B is at vertical distance -1
• Node C is right child of node A
  • Distance of C Node is incremented by 1, (0 + 1) so it becomes 1
    • Node C is at vertical distance 1

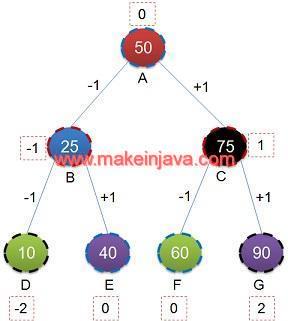
Example 2: Vertical order distance of binary tree in java

• Node A is at distance 0
• Node B is left child of Node A
  • Node B is at vertical distance -1
  • Node D is left child of Node B (Node B is at distance -1)
    • Node D is at vertical distance -2
  • Node E is right child of Node B (Node B is at distance -1)
    • Node E is at vertical distance 0 (-1  + 1 = 0)
• Node C is right child of Node A (at vertical distance 0)
  • Vertical distance of Node C is 1
  • Vertical distance of Node F is 0
  • Vertical distance of Node G is 2

Algorithm to find vertical distance in a binary tree using java

• Initialize the distance 0 for root node
• Create a HashMap of Vertical distance and List of nodes
  • Map<Integer, List<Integer>> mapVerticalDistance
• Perform the pre order traversal of binary tree
  • If, hashmap does not contains distance
    • Add distance and node value to hashmap
  • else, update for hashmap for corresponding distance
  • Perform traversal for left child of
    • Decrements the distance by -1 & traverse binary tree
  • Perform traversal for right child of
    • Increment the distance by 1 & traverse binary tree.
• At end of recursive operation, we would get vertical distance of all nodes.

Time complexity of algorithm is O(n).

Program – Vertical order traversal of a binary tree (recursive) using java

1.) VerticalOrderOfBTree class:

• VerticalOrderOfBTree class is responsible, for printing the binary tree in vertical order.

package org.learn.Question;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class VerticalOrderOfBTree {
 private static Map<Integer, List<Integer>> mapVerticalDistance = null;

 private static void verticalOrder(Node root, int distance) {
  if (null == root)
   return;

  List<Integer> list = null;
  if (mapVerticalDistance.containsKey(distance)) {
   list = mapVerticalDistance.get(distance);
  } else {
   list = new ArrayList<Integer>();
  }
  
  list.add(root.data);
  mapVerticalDistance.put(distance, list);
  verticalOrder(root.left, distance - 1);
  verticalOrder(root.right, distance + 1);
 }

 public static void verticalOrderOfBTree(Node root) {
  
  if (null == mapVerticalDistance) {
   mapVerticalDistance = new HashMap<Integer, List<Integer>>();
  } else {
   mapVerticalDistance.clear();
  }
  
  verticalOrder(root, 0);
  mapVerticalDistance
    .forEach(
      (k, v) 
       -> System.out.println("Nodes at distance " + k + " = " + v));
 }
}

2.) Node Class:

• Node class is representing the nodes of a binary tree.

package org.learn.Question;

public class Node {
 public int data;
 public Node left;
 public Node right;

 public Node(int num) {
  this.data = num;
  this.left = null;
  this.right = null;
 }

 public Node() {
  this.left = null;
  this.right = null;
 }
 
 public static Node createNode(int number) {
  return new Node(number);
 }
}

3.) App Class:

• We are constructing the binary tree in main method.
• We are calling VerticalOrderOfBTree  class to print binary tree in vertical order.

package org.learn.Client;

import org.learn.Question.Node;
import org.learn.Question.VerticalOrderOfBTree;

public class App {
 public static void main(String[] args) {
  // root level 0
  Node A = Node.createNode(50);
  // Level 1
  Node B = Node.createNode(25);
  Node C = Node.createNode(75);
  // Level 2
  Node D = Node.createNode(10);
  Node E = Node.createNode(40);
  Node F = Node.createNode(60);
  Node G = Node.createNode(90);

  // connect Level 0 and 1
  A.left = B;
  A.right = C;
  // connect level 1 and level 2
  B.left = D;
  B.right = E;
  C.left = F;
  C.right = G;

  VerticalOrderOfBTree.verticalOrderOfBTree(A);
 }
}

Output – vertical order traversal of binary tree using java

Nodes at distance 0 = [50, 40, 60]
Nodes at distance -1 = [25]
Nodes at distance -2 = [10]
Nodes at distance 1 = [75]
Nodes at distance 2 = [90]

Download Code – print binary tree in Vertical Order (DFS)