Prime number generator in java using Sieve of Eratosthenes algorithm

• A prime number is a natural number greater than 1 that has no positive divisors other than 1 & itself.
  • e.g.Number 7 is prime number because 7 have two factor i.e. 1 & 7
  • e.g.Number 4 is not prime number because 4 have factors of 1, 2 & 4.
  • List of prime numbers from 0 – 30 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
• Sieve of Eratosthenes is a simple algorithm for finding prime numbers up to given limit.
• Sieve of Eratosthenes algorithm is based upon elimination technique.
•  The algorithm iteratively eliminates the composite numbers, which are multiple of each prime.

Algorithm – find prime numbers till given number ( 2 to number)

• Create a list of consecutive integers from 2 through n: (2, 3, 4, …, n).
• Initially, let p equal 2, the smallest prime number.
• Enumerate the multiples of p by counting to n from 2p in increments of p, and mark them in the list (these will be 2p, 3p, 4p, … ; the p itself should not be marked).
• Find the first number greater than p in the list that is not marked. If there was no such number, stop. Otherwise, let p now equal this new number (which is the next prime), and repeat from step 3.

Example: Prime numbers using Sieve of Eratosthenes algorithm

• Generate the prime numbers till 30 ( from 2 to 30)

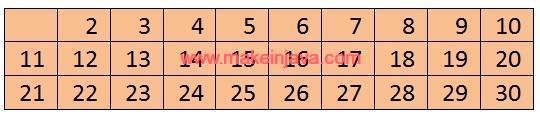
• First number in the table is 2, so eliminates all number multiple of 2.

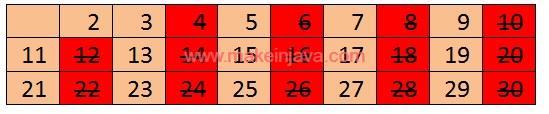
• Second number in table is 3, so eliminates all number multiple of 3.

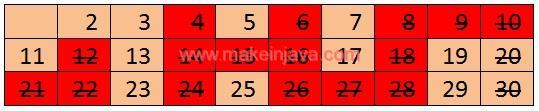
• Next number in table is 5, so eliminates all number multiple of 5.

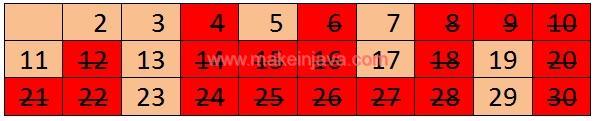
The unmarked numbers in the table are prime numbers till 30: 2 3 5 7 11 13 17 19 23 29

Program: prime number generator in java using Sieve of Eratosthenes algorithm

package org.learn.arrays;

import java.util.Arrays;
import java.util.Scanner;

public class SieveEratosthenes {
 public static void generatePrimeNumbers(int maxNumber) {

  boolean[] isPrime = new boolean[maxNumber + 1];
  Arrays.fill(isPrime, true);

  int primeRange = (int) Math.sqrt(maxNumber);
  for (int number = 2; number <= primeRange; number++) {
   if (isPrime[number]) {
    for (int iEliminate = number * number; iEliminate <= maxNumber; iEliminate += number) {
     isPrime[iEliminate] = false;
    }
   }
  }
  int number = 2;
  while (number <= maxNumber) {
   if (isPrime[number]) {
    System.out.printf("%d ", number);
   }
   number++;
  }

  return;
 }

 public static void main(String[] args) {

  try (Scanner scanner = new Scanner(System.in)) {
   System.out.print("1. Enter the number:  ");
   int maxNumber = scanner.nextInt();
   System.out.printf("2. Prime numbers till %d : ", maxNumber);
   generatePrimeNumbers(maxNumber);
  }
 }
}

Output: prime numbers in java using Sieve of Eratosthenes algorithm

1. Enter the number:  30
2. Prime numbers till 30 : 2 3 5 7 11 13 17 19 23 29 

1. Enter the number:  50
2. Prime numbers till 50 : 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47