Veritcal Order Sum in a binary tree
- Given a binary tree, find out a vertical order sum using recursive algorithm.
- Traverse the binary tree using depth first search (dfs) algorithm.
- The nodes, which are at same vertical distance, are said to be on same vertical path.
- The root node is assumed to be at vertical distance of 0.
- When, we traverse left subtree, we decrements the vertical distance by 1.
- When, we traverse right subtree, we increment the vertical distance by 1.
- We have discussed similar problem Vertical order traversal in a binary tree
Examples – find vertical order sum in a binary tree using java.
Example 1: calculate vertical order sum using recursive algorithm
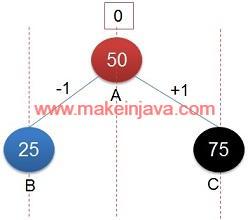
- Node A is at distance 0.
- Sum at distance 0 = 50
- Node B is left child of node A
- Distance of B Node is decremented by 1.
- Node B is at vertical distance -1
- Sum at vertical distance -1 = 25
- Distance of B Node is decremented by 1.
- Node C is right child of node A
- Distance of C Node is incremented by 1, (0 + 1) so it becomes 1
- Node C is at vertical distance 1
- Sum at vertical distance 1 = 75
- Distance of C Node is incremented by 1, (0 + 1) so it becomes 1
The vertical order sum of binary tree (Fig 1) is as follows:
| S. No. | Vertical distance | Node | Sum |
|---|---|---|---|
| 1 | 0 | A | 50 |
| 2 | -1 | B | 25 |
| 3 | 1 | C | 75 |
Example 2: find vertical sum of binary tree using depth first search
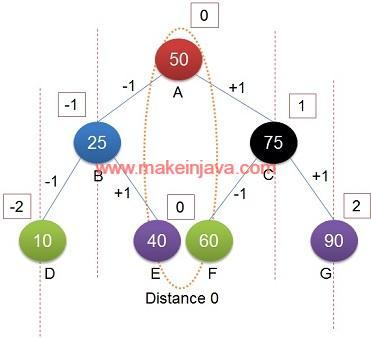
- Node A is at distance 0
- Node B is left child of Node A
- Node B is at vertical distance -1
- Node D is left child of Node B (Node B is at distance -1)
- Node D is at vertical distance -2
- E is right child of B (Node B is at distance -1)
- So, Node E is currently showing value of 0 (-1 + 1 = 0)
- Node C is right child of A (at vertical distance 0)
- Vertical distance of Node C is 1
- Vertical distance of Node F is 0
- Vertical distance of Node G is 2
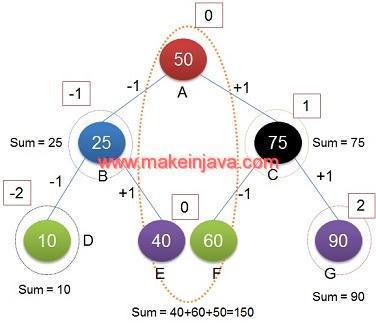
Once we know the vertical distance of each nodes, we can simply add the sum of nodes at same vertical distance. The vertical order sum of binary tree (shown in Fig 2) is as follows:
| S. No. | Vertical distance | Node(s) | Sum |
|---|---|---|---|
| 1 | 0 | A, E, F | 50+40+6=150 |
| 2 | -1 | B | 25 |
| 3 | -2 | D | 10 |
| 4 | 1 | C | 75 |
| 5 | 2 | G | 90 |
Code – vertical order sum of a binary tree in java (recursive / DFS)
1.) VerticalOrderSumOfBTree class:
- VerticalOrderSumOfBTree class is responsible for calculating the sum of nodes.
- Traverse the binary tree using vertical order traversal (recursive method).
package org.learn.Question;import java.util.HashMap;import java.util.Map;public class VerticalOrderSumOfBTree { private static Map<Integer, Integer> map = null; private static void verticalOrder(Node root, int distance) { if (null == root) return; int existingValue = 0; if (map.containsKey(distance)) { existingValue = map.get(distance); } map.put(distance, root.data + existingValue); verticalOrder(root.left, distance - 1); verticalOrder(root.right, distance + 1); } public static void verticalOrderSumOfBTree(Node root) { if (null == map) { map = new HashMap<Integer, Integer>(); } else { map.clear(); } verticalOrder(root, 0); map.forEach((k, v) -> System.out.println("Nodes at distance " + k + " = " + v)); }} |
2.) Node Class:
- Node class is representing the nodes of a binary tree.
package org.learn.Question;public class Node { public int data; public Node left; public Node right; public Node(int num) { this.data = num; this.left = null; this.right = null; } public Node() { this.left = null; this.right = null; } public static Node createNode(int number) { return new Node(number); }} |
3.) App Class:
- We are constructing the binary tree in a main method.
- Find out sum of nodes using vertical order traversal.
package org.learn.Client;import org.learn.Question.Node;import org.learn.Question.VerticalOrderSumOfBTree;public class App { public static void main(String[] args) { // root level 0 Node A = Node.createNode(50); // Level 1 Node B = Node.createNode(25); Node C = Node.createNode(75); // Level 2 Node D = Node.createNode(10); Node E = Node.createNode(40); Node F = Node.createNode(60); Node G = Node.createNode(90); // connect Level 0 and 1 A.left = B; A.right = C; // connect level 1 and level 2 B.left = D; B.right = E; C.left = F; C.right = G; VerticalOrderSumOfBTree.verticalOrderSumOfBTree(A); }} |
Output – vertical order sum of a binary tree using java (recursion/dfs)
Nodes at distance 0 = 150Nodes at distance -1 = 25Nodes at distance -2 = 10Nodes at distance 1 = 75Nodes at distance 2 = 90 |
