Find or search node in a binary search tree (Java/ recursive /example)

• Given a binary search tree, we would like to find or search element in BST
  • Traverse the binary search tree using depth first search(DFS) recursive algorithm.
• If we were given a binary tree (not BST), then we need to traverse all nodes to find element.
  • But, In case of BST, We are not required to traverse the all nodes of BST.
• BST has following properties.
  • Left child of binary tree is less than its parent node
  • Right child of binary tree is greater than its parent node
• At every node, we will take a decision whether to go towards left subtree or right subtree.

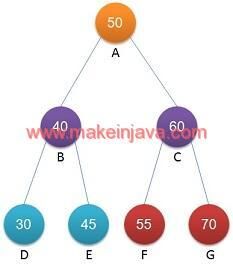
• If we would like to search node, having value 70
  • Then program should return Node G
• If we would like to search node having value 40
  • The program should return Node B

Example – Search node having value = 45 in binary search tree using java

1. Traverse binary search tree using DFS algorithm
2. Compare input value (45) with every node of BST.
3. At every node, we will make decision about the traversal of BST
   • Input number is equal node data (We found the element).
   • Input number is less than node data
     • Find the element in left subtree.
   • Input number is greater than node data.
     • Find the element in right subtree.

The condition to find element in binary search tree is as follows.

  //Condition 1. we found the element
  if(node.data == value) {
   return node;
  } 
  //Condition 2. 
  //Value is less than node value. so go left sub tree
  else if(value < node.data)
     return findNodeInBST(node.left,value);
  //Condition 3. 
  //Value is greater than node value. so go right sub tree
  else 
     return findNodeInBST(node.right,value);

Algorithm: find element in a binary search tree using recursive method

• Find element having value 45 and go to root node A (Fig 2)
• Apply condition at Node A
  •   45 == 50 ? Not true & check next condition
  •   45 < 50 ? True , Traverse left subtree to find element (45).
    • Got to node B (value at node B is 0) and equate with node data.
      • 45 == 40. false & check next condition
      • 45 < 40 false & check next condition
      • 45 > 40, true Yes (Condition is satisfied)
        • Go to right subtree (Node E) to find element (45)
        • Apply condition at Node E
          •   45 == 45
            • return from here (return Node E from here)
      • At Node B
        • return Node E (which we got from right sub tree)
  • At Node A
    • return Node E.
• We found the Node E

Program: find element or node in a binary search tree (java / recursive)

1.) FindNodeInBST Class:

• FindNodeInBSTclass is used to find the element or node in a binary search tree (BST).
• Traverse the binary search tree using recursive algorithm

package org.learn.Question;

public class FindNodeInBST {
 public static Node findNodeInBST(Node node, int value) {
  if(null == node) {
   return null;
  }
  //Condition 1. we found the value
  if(node.data == value) {
   return node;
  } 
  //Condition 2. 
  //Value is less than node value. so go left sub tree
  else if(value < node.data)
   return findNodeInBST(node.left,value);
  //Condition 3. 
  //Value is greater than node value. so go right sub tree
  else 
   return findNodeInBST(node.right,value);
 }
}

2.) Node Class:

• Node class representing the node(s) of a binary search tree.

package org.learn.Question;

public class Node {
 public int data;
 public Node left;
 public Node right;

 public Node(int num) {
  this.data = num;
  this.left = null;
  this.right = null;
 }

 public Node() {
  this.left = null;
  this.right = null;
 }

 public static Node createNode(int number) {
  return new Node(number);
 }
}

3.) App Class: 

• We are constructing binary search tree in a main method.
• We are calling the method of FindNodeInBST class, to find or search the node in a binary search tree.

package org.learn.Client;

import org.learn.Question.FindNodeInBST;
import org.learn.Question.Node;

public class App {
 public static void main(String[] args) {
  // root level 0
  Node A = Node.createNode(50);
  // Level 1
  Node B = Node.createNode(40);
  Node C = Node.createNode(60);
  // Level 2
  Node D = Node.createNode(30);
  Node E = Node.createNode(45);
  Node F = Node.createNode(55);
  Node G = Node.createNode(70);

  // connect Level 0 and 1
  A.left = B;
  A.right = C;
  // connect level 1 and level 2
  B.left = D;
  B.right = E;
  C.left = F;
  C.right = G;
    
  Node node = FindNodeInBST.findNodeInBST(A, 180);
  if (null == node) {
   System.out.printf("Node=%d does not exists in BST\n",180);
  } else {
   System.out.printf("Found node=%d in BST\n",180);
  }
  
  node = FindNodeInBST.findNodeInBST(A, 45);
  if (null == node) {
   System.out.printf("Node=%d does not exists in BST\n",45);
  } else {
   System.out.printf("Found node=%d in BST\n",45);
  }
 }
}

Output – find or search node in a BST (Java /recursive algorithm)

Node=180 does not exists in BST
Found node=45 in BST

Download code – find or search a Node in BST Java recursive algorithm