- Given a binary tree having multiple paths from root to leaf nodes.
- Find out a path in a binary tree, having sum equals to given input number.
- We will use depth first search (Pre Order) to traverse the binary tree.
- We have discussed similar problem to print all paths from root to leaf.
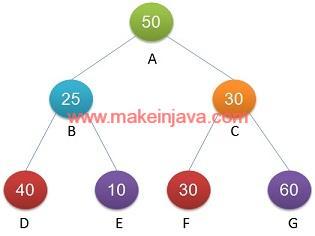
The binary tree shown in Fig 1, has four root to leaf paths. We have shown the paths in following table.
| S. No. | Root to leaf path | Path Sum |
|---|---|---|
| 1 | A -> B -> D | 105 |
| 2 | A -> B -> E | 85 |
| 3 | A -> C -> F | 110 |
| 4 | A -> C -> G | 140 |
Example: find a root to leaf path, sum equals to number 110.
- Traverse the binary tree, using depth first search (PreOrder traversal).
- During DFS traversal, at every node, deduct node value from input number.
- Pass the resultant value to its children (left and right subtree).
- When we encounter the leaf node, the resultant value will reduced to zero (if path exist).
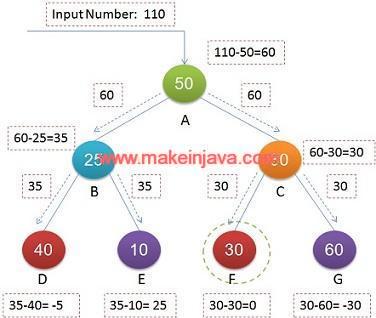
- We have shown algorithm in Fig 2.
Let us look into the binary tree, shown in Fig 2. We are subtracting the respective node value at each level. We can see that leaf node F is having value equals 0. So, A->C->F is root to leaf path, having sum equals 110.
Algorithm – root to leaf path, sum equals to number
- Declare array (arr) containing the root to leaf path.
- Perform DFS traversal (pre order)
- Save current node value in arr
- Subtract the current node value from given number
- If given number is 110 and node value is 50.
- then, effective value is 110 – 50 = 60.
- If given number is 110 and node value is 50.
- The subtracted value should be pass to it child nodes.
- Perform binary tree traversal for left & right subtree.
- Keep on traversing the binary tree, till we reach the leaf.
- At leaf node, check the value (after deducting current node value).
- If value is 0, We found the path.
- Save the path in arr and return.
- If value is not 0, Keep traversing the binary tree.
- If value is 0, We found the path.
- At leaf node, check the value (after deducting current node value).
- At end of traversal, we will get, root to leaf path, sum equals to input number (if path exists).
- Time complexity: O(n)
Program – Root to leaf path, sum equals to given number
1.) SumInRoot2LeafPath Class : SumInRoot2LeafPath class is responsible, for finding the path, having sum equals to given number.
package org.learn.Question;import java.util.Arrays;public class SumInRoot2LeafPath { private static int[] arr; public static void sumInRoot2LeafPath(Node root, int[] path,int sum) { boolean sumExist = sumInRoot2LeafPath(root, path,0,sum); if(sumExist) { System.out.println("Sum exists in Path: " + Arrays.toString(arr)); } else { System.out.println("Sum does not exist in any Path"); } } private static boolean sumInRoot2LeafPath(Node root, int[] path,int index,int sum) { if(null == root) { return false; } path[index++] = root.data; sum = sum - root.data; if(root.left == null && root.right == null) { if(sum == 0) { arr = Arrays.copyOf(path, index); return true; } return false; } return sumInRoot2LeafPath(root.left,path,index,sum ) || sumInRoot2LeafPath(root.right,path,index,sum ); } } |
2.) Node Class : Node class representing the nodes of binary tree.
package org.learn.Question;public class Node { public int data; public Node left; public Node right; public Node(int num) { this.data = num; this.left = null; this.right = null; } public Node() { this.left = null; this.right = null; } public static Node createNode(int number) { return new Node(number); }} |
3.) App Class:
- We are constructing the binary tree in main method.
- We are calling sumInRoot2LeafPath method to print, root to leaf path, sum equals to given number.
package org.learn.Client;import org.learn.Question.Node;import org.learn.Question.SumInRoot2LeafPath;public class App { public static void main( String[] args ) { Node root = Node.createNode(50); root.left = Node.createNode(30); root.right = Node.createNode(30); // left sub tree root.left.left = Node.createNode(40); root.left.right = Node.createNode(10); // right subtree root.right.left = Node.createNode(30); root.right.right = Node.createNode(60); int[] path = new int[512]; SumInRoot2LeafPath.sumInRoot2LeafPath(root,path,110); }} |
Output – Root to leaf path, sum equals to input number
Sum exists in Path: [50, 30, 30] |
Download Code – Root to leaf path, Sum equals given number
