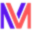- Given a binary tree, find out maximum width of a binary tree using non recursive algorithm.
- Traverse the binary tree using breadth first search (BFS) or level order traversal algorithm.
- What is width of a binary tree?
- The number of nodes at any level gives the width of binary tree (at that level)
- Calculate the width at each level of binary tee.
- The maximum among the widths, calculate at each level, is maximum width of binary tree.
- We have discussed the similar problem Find Level in binary tree having maximum sum.
Example: find width of binary tree bfs algorithm
- Traverse the binary tree using level order traversal.
- Calculate the width at each level.
- Maximum width = max (level 1, ,level 2 …level n)
Let us calculate the width at each level. The table is showing the width at each level.
| Level | Width |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 2 |
Algorithm – calculate width of binary tree (level order traversal)
We will use breadth first search or level order traversal to iterate through the binary tree.
- Create variable maxWidth=0 for maximum width of binary tree
- Create variable to localWidth=0 for width at each level
- Insert root to queue
- Add null to the queue (level delimiter)
- Iterate through the Queue
- Pop node from queue & check for null
- We are at next level & compare localWidth of current level with maxWidth
- If localWidth is more than maxWidth then update maxWidth
- Reset localWidth to zero
- Add next level children (left and right child)
- Increment width of current level by 1 (localWidth++)
- Pop node from queue & check for null
- Once we exit the loop, we will get the maximum width.
Program – calculate width of binary tree (level order traversal)
1.) MaxWidthOfBTree Class: MaxWidthOfBTree class is used to find the maximum width of a binary tree.
package org.learn.Question;
import java.util.LinkedList;
import java.util.Queue;
import org.learn.PrepareTree.Node;
public class MaxWidthOfBTree {
public static void maxWidthOfBTree(Node root) {
if (root == null) {
System.out.println("Tree is empty");
return ;
}
Queue<Node> queue = new LinkedList<Node>();
queue.offer(root);
//level delimiter
queue.offer(null);
int maxWidth = 0;
int level = 0;
//default root level
int localLevel = 0;
int localWidth = 0;
while (!queue.isEmpty()) {
Node node = queue.poll();
//Level change
if (null == node) {
if (!queue.isEmpty()) {
//level delimiter
queue.offer(null);
}
if(localWidth > maxWidth) {
maxWidth = localWidth;
level = localLevel;
}
//Reset the level sum for next level calculation
localWidth = 0;
localLevel ++;
} else {
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
localWidth ++;
}
}
System.out.printf("Max Width %d is at level %d \n",maxWidth,level);
return;
}
}
2.) Node Class: The class representing the nodes of a binary tree.
package org.learn.PrepareTree;
public class Node {
public int data;
public Node left;
public Node right;
public Node(int num) {
this.data = num;
this.left = null;
this.right = null;
}
public Node() {
this.left = null;
this.right = null;
}
public static Node createNode(int number)
{
return new Node(number);
}
}
3.) App Class: We are creating the binary tree in a main method & calling the method of MaxWidthOfBTree class, to find the maximum width in a binary tree.
package org.learn.Client;
import org.learn.PrepareTree.Node;
import org.learn.Question.MaxWidthOfBTree;
public class App
{
public static void main( String[] args )
{
//root level 0
Node A = Node.createNode(100);
//Level 1
Node B = Node.createNode(50);
Node C = Node.createNode(150);
//Level 2
Node D = Node.createNode(25);
Node E = Node.createNode(75);
Node F = Node.createNode(125);
Node G = Node.createNode(175);
//Level 3
Node H = Node.createNode(120);
Node I = Node.createNode(140);
//connect Level 0 and 1
A.left = B;
A.right = C;
//connect level 1 and level 2
B.left = D;
B.right = E;
C.left = F;
C.right = G;
//Connect level 2 and level 3
F.left = H;
F.right = I;
MaxWidthOfBTree.maxWidthOfBTree(A);
}
}
Output – width of binary tree using non recursive algorithm
Max Width 4 is at level 2
Download Code – calculate max width of binary tree(BFS)