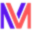- Given a binary search tree (bst), find inorder predecessor using iterative algorithm.
- What is InOrder predecessor in BST?
- InOrder predecessor of given node is largest key, smaller than input node in BST.
- We have discussed similar problem find inorder successor in binary search tree.
Inorder traversal of binary search tree
25 50 75 100 120 125 140 150 160 175 190
InOrder traversal of binary search tree, gives the sorted output. So, predecessor node is immediate smaller node of input node. Let us take some examples to find predecessor of any input node:
| S. No. | Input node | Predecessor node |
|---|---|---|
| 1 | Node H (120) | Node A (100) |
| 2 | Node E (75) | Node B (50) |
| 3 | Node F (125) | Node H(120) |
| 4 | Node C (150) | Node I(140) |
Algorithm – find inorder predecessor node in parent nodes
- Traverse the parents nodes.
- Check input node is on right subtree of parent node.
- If we can find such parent node, then
- Parent node will be InOrder predecessor node.
- If we can find such parent node, then
Examples – InOrder predecessor in binary search tree (BST) using java
Example 1: find inorder predecessor of Node H (120) in BST
Node A (100) is predecessor node of Node H. Node H does not have any left child, so predecessor of Node H will lie in its parent nodes. We will traverse up the binary search tree, where we can find the parent node, to whom Node H lies in right subtree (e.g Node A).
- Go to parent of Node H i.e. Node F
- Is Node H lying on the right subtree of Node F?
- No
- Go to parent of Node F i.e. Node C
- Is Node H lying on the right sub tree of Node C?
- No
- Is Node H lying on the right sub tree of Node C?
- Go to parent of Node C i.e. Node A
- Is Node H is on the right sub tree of Node A
- Yes, Node A is predecessor of Node H
- Is Node H is on the right sub tree of Node A
Example 2: find inorder predecessor of Node E (75) in BST
Node B will be predecessor node of Node E.
Node E does not have any left child, so predecessor of Node E will lie in its parent nodes. This example is exactly similar to example 1. So let us apply the same algorithm here.
- Go to parent of Node E i.e. Node B
- Is Node E lying in right sub tree of Node B ?
- Yes, Node B is predecessor of Node E
Example 3: find inorder predecessor of Node F (125) in bst.
Node H (120) is predecessor node of Node F
- Node F has left child.
- so predecessor will be lying in the left sub tree of Node F.
- Find the maximum element in the left subtree of Node F.
- Node F has only one child i.e. Node H.
- Predecessor of Node F is Node H.
Example 4: find inorder predecessor of Node C (150) in bst
- Node C has left child
- InOrder predecessor of Node C is lying in the left sub tree.
- Find the maximum element in the left subtree of Node C.
- Node I is maximum element in the left subtree of Node C.
- Node I become the InOrder predecessor of Node C.
We can conclude our algorithms from above examples. We can categorize algorithm into following categories
- Find predecessor of node, who do not have any left child
- Example 1 and Example 2
- Find predecessor of node, who have left child node
- Example 3, Example 4
Algorithm – InOrder predecessor in binary search tree (BST).
we will have couple of basic conditions to find the inorder predecessor in binary search tree.
- Got the root of binary tree and node (whose predecessor we are looking for)
- Check node have left child (Example 3 to example 5)
- If it have left child
- Immediate smaller node or inorder predecessor is in left sub tree only.
- Find the maximum element in the left subtree
- Return the inorder predecessor
- If left child null
- So, inorder is lying some where in parents
- Example 1 and Example 2
- Now go to parents and search predecessor node.
- So, inorder is lying some where in parents
- If it have left child
- Find inorder predecessor in parent nodes.
- Start scanning the binary search tree from root.
- As we have to search the inorder in parents (of input node)
- So, equality of root data with input node, will be our exit condition
- As, we would have found the node before reaching input node
- If we encounter right child ( simple scanning of BST)
- Save it as inorder predecessor, we are interested in right child only.
- As discussed in example 1 and example 2
- Save it as inorder predecessor, we are interested in right child only.
- If we encounter left child, keep Scanning the tree.
- At end of scanning, we will have InOrder predecessor.
- Time Complexity : O(h)
Program – find inorder predecessor in a binary search tree using java.
1.) InorderPredecessor class:
- InorderPredecessor class is used to find inorder predecessor of given node
package org.learn.Question;
public class InorderPredecessor {
private static Node max(Node root) {
// we found the max node
if (root.right == null) {
return root;
}
return max(root.right);
}
public static Node predecessor(Node root, Node node) {
// Example 3 or Example 4
if (node.left != null)
return max(node.left);
// Example 1 or Example 2
Node predecessor = null;
// Start from root and search for predecessor down the tree
while (root != null) {
if (node.data == root.data) {
// by now we might found our predecessor
break;
} else if (node.data < root.data) {
root = root.left;
} else if (node.data > root.data) {
predecessor = root;
root = root.right;
}
}
return predecessor;
}
}
2.) Node class:
- Node class representing the nodes of a binary search tree.
package org.learn.Question;
public class Node {
public int data;
public Node left;
public Node right;
public Node(int num) {
this.data = num;
this.left = null;
this.right = null;
}
public Node() {
this.left = null;
this.right = null;
}
public static Node createNode(int number) {
return new Node(number);
}
}
3.) App class:
- We are constructing binary tree in main method.
- We are calling method of InorderPredecessor class to find inorder predecessor for any given node.
package org.learn.Client;
import org.learn.Question.InorderPredecessor;
import org.learn.Question.Node;
public class App {
public static void main(String[] args) {
// root level 0
Node A = Node.createNode(100);
// Level 1
Node B = Node.createNode(50);
Node C = Node.createNode(150);
// Level 2
Node D = Node.createNode(25);
Node E = Node.createNode(75);
Node F = Node.createNode(125);
Node G = Node.createNode(175);
// Level 3
Node H = Node.createNode(120);
Node I = Node.createNode(140);
Node J = Node.createNode(160);
Node K = Node.createNode(190);
// connect Level 0 and 1
A.left = B;
A.right = C;
// connect level 1 and level 2
B.left = D;
B.right = E;
C.left = F;
C.right = G;
// Connect level 2 and level 3
F.left = H;
F.right = I;
G.left = J;
G.right = K;
Node predecessor = InorderPredecessor.predecessor(A, H);
System.out.printf("Inorder predecessor of Node %d is %d\n", H.data, predecessor.data);
predecessor = InorderPredecessor.predecessor(A, E);
System.out.printf("Inorder predecessor of Node %d is %d\n", E.data, predecessor.data);
predecessor = InorderPredecessor.predecessor(A, F);
System.out.printf("Inorder predecessor of Node %d is %d\n", F.data, predecessor.data);
predecessor = InorderPredecessor.predecessor(A, C);
System.out.printf("Inorder predecessor of Node %d is %d\n", C.data, predecessor.data);
predecessor = InorderPredecessor.predecessor(A, A);
System.out.printf("Inorder predecessor of Node %d is %d\n", A.data, predecessor.data);
}
}
Output – InOrder predecessor in binary search tree (BST) using java
Inorder predecessor of Node 120 is 100 Inorder predecessor of Node 75 is 50 Inorder predecessor of Node 125 is 120 Inorder predecessor of Node 150 is 140 Inorder predecessor of Node 100 is 75