What is factorial of number?
- Factorial of a non-negative integer n, denoted by n!.
- Factorial is the product of all positive integers less than or equal to n.
- 0! = 1
- 1! = 1
- 3! = 3 * 2 * 1 = 6
- 6! = 6 * 5 * 4 * 3 * 2 * 1 = 120
- n! = n * n – 1! = n * n – 1 * n – 2 ! and so on
- We would like to find factorial of a given number using recursive & iterative algorithm in java.
Algorithm to find factorial using recursive algorithm
- Calculate then factorial of number = 5.
- We know 0! = 1, our base condition.
- Also, We know n! = n * n – 1! = n * n – 1 * n – 2 ! and so on
- Find factorial using point 3.
- i.e. factorial (n) = n * factorial (n-1)
- factorial (5) = 5 * factorial (4)
- 5 * 4 * factorial (3).
- 5 * 4 * 3 * factorial (2).
- 5 * 4 * 3 * 2 * factorial (1) = 120.
- We have shown the demonstration of recursive algorithm in Fig 1.

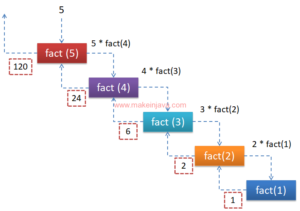 Fig 1: Factorial of 5
Fig 1: Factorial of 5
Program to find factorial using recursive & iterative algorithm
package org.learn;
import java.util.Scanner;
public class DemoFactorial {
private static int factRecursive(int number) {
// base condition
if (number == 1)
return 1;
// calculate the factorial of all number
return number * factRecursive(number - 1);
}
private static int factIterative(int number) {
int factorial = 1;
for (int iNumber = 1; iNumber <= number; iNumber++) {
factorial = factorial * iNumber;
}
return factorial;
}
public static void main(String[] args) {
try (Scanner scanner = new Scanner(System.in)) {
/* Calculate factorial for input number */
System.out.printf(" Enter input number : ");
int number = scanner.nextInt();
int factNumber = factRecursive(number);
System.out.printf("factorial(%d) - Recursive method: %d\n",number,factNumber);
factNumber = factIterative(number);
System.out.printf("factorial(%d) - Iterative method: %d\n",number,factNumber);
}
}
}
Output: Factorial of a number – recursive & iterative method is:
Enter input number : 5
factorial(5) - Recursive method: 120
factorial(5) - Iterative method: 120
Enter input number : 7
factorial(7) - Recursive method: 5040
factorial(7) - Iterative method: 5040