Find element in an array using binary search algorithm in java (recursive)

• Binary search is a divide and conquer algorithm.
  • Divide and conquer algorithm is process of dividing the input data-set after each iteration.
• Binary search algorithm works on sorted arrays.
  • We can not apply the binary search to unsorted array.
• We will use the recursive method to find element in an array.
• In binary search algorithm, after each iteration the size of array is reduced by half.

Algorithm – find element in an array using binary search algorithm

Given an sorted array as shown in Fig 1, we would like to find element 70 in an array.  The algorithm is as follows:

• Divide the input array into two halves.
  • We will create two indexes low and high.
• low will points to the lowest index in an array
• high will points to the highest index in an array
• mid will points to the mid point of an array.
• In every iteration, we will reduced the input array by half
  • That’s why it is divide and conquer algorithm
• Time complexity is log(N)

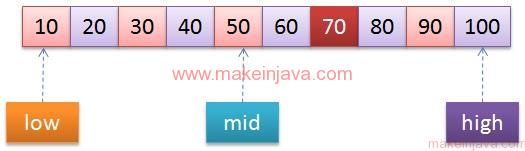
Step 1: find element 70 in an input array using binary search algorithm

• low points to 10
• high points 100
• mid = low + (high – low) / 2
• Is 70 < 50 ?
  • No
• Is 70 > 50 ?
  • Yes
  • Search element in upper array [60 to 100]
  • We will ignore lower half of array (low to mid).

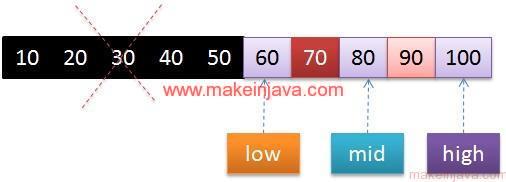
Step 2: find element 70 in an array using binary search algorithm.

• In step 1, we have ignored the first half of an array.
  • So, lets us update low index.
• low points to 60
• high points to 100
• mid = low + (high – low) / 2
  • mid points to 80
• Is 70 < 60 ?
  • No
• Is 70 > 60 ?
  • Yes
  • Search element in lower half [60 to 80]
  • We will ignore the upper half.

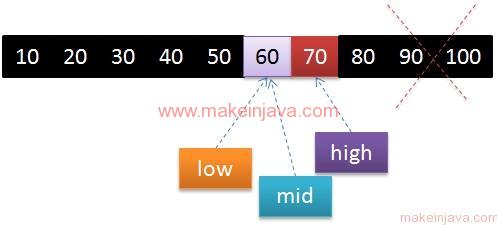
Step 3: find element using binary search algorithm in java.

• Similar to step no 2

Step 4: find element using binary search algorithm in java.

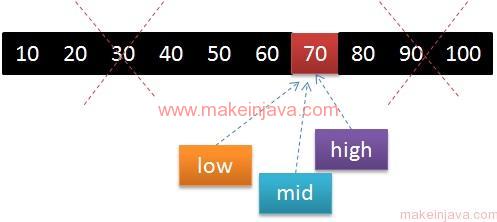
• After apply the iterations as shown in above steps, we will left with 70 element
• low point to 70
• high point 70
• mid = low + (high – low) / 2
  • mid points to 70
• mid will point to 70
• We will get the element desired element.

Program: find element in an array using binary search recursive algorithm

package org.learn.arrays;

public class BinarySearchRecursive {
	public static void main(String[] args) {
		int arr[] = {10,20,30,40,50,60,70,80,90,100};
		//low index
		int low = 0;
		//high index
		int high = arr.length - 1;
		int search = 70;
		int result = binarySearch(arr, search, low, high);
		if(result == -1) {
			System.out.printf("Element %d not found in array",search);			
		} else {
			System.out.printf("Element %d found at index : %d ",search,result);
		}
		System.out.println("");
		
		search = 60;
		result = binarySearch(arr, search, low, high);
		if(result == -1) {
			System.out.printf("Element %d not found in array",search);			
		} else {
			System.out.printf("Element %d found at index : %d",search,result);
		}
		System.out.println("");
		
		search = 110;
		result = binarySearch(arr, search, low, high);
		if(result == -1) {
			System.out.printf("Element %d not found in array",search);			
		} else {
			System.out.printf("Element %d found at index : %d",search,result);
		}
		System.out.println("");
	}

	private static int binarySearch(int[] arr, int value, int low, int high) {
		if (high < low)
			return -1;
		
		int middle = low + (high - low) / 2;
		if (value < arr[middle]) { // search between low ---> middle - 1
			return binarySearch(arr, value, low, middle - 1);
		} else if (value > arr[middle]) {
			//search in upper half middle + 1 -----> high
			//low to middle already covered in first case
			// so start search from middle + 1 to high here...
			return binarySearch(arr, value, middle + 1, high);
		} else {
			// value == arr[middle]
			//yes we got the element in binary search tree
			return middle;
		}	
	}
}

Output – element in an array in java (binary search recursive algorithm)

Element 70 found at index : 6
Element 60 found at index : 5
Element 110 not found in array