- Given a key or number, we would like to delete a node from in binary search tree (BST).
- We will delete the node from BST using depth first search recursive algorithm.
- We have already discussed to delete binary tree using DFS.
- The algorithm is virtually divided into three parts. We will discuss each part with examples.
- We will search the node in BST and then we will delete the node.
- We will have following different conditions:
- Node to be deleted, is a leaf node of BST. [Refer Example 1]
- Node having no children (node.left == null and node.right == null)
- Node to be deleted having one child node. [Refer Example 2]
- Node having either left child or right child.
- Node to be deleted having both left and right child. [Refer Example 3]
- Node to be deleted, is a leaf node of BST. [Refer Example 1]
Examples – delete a node from binary search tree (bst) using java
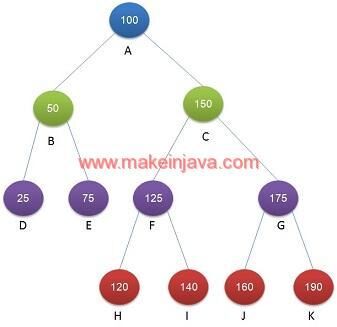
Example 1: Delete leaf node E from BST using java
- Delete the Node from binary tree having value 75 (Node E).
- Search or find a node in BST
- node.data == 75
- Found node E in BST
- Delete Node E from BST
- Set Right child of Node B as null
Example 2: Remove Node having one child from BST in java
- We would like to delete Node B from BST.
- Node B is child node so we can not directly remove the node B.
- We will follow the below procedure to delete the node B.
- Search the node (Node B) in BST to be deleted
- node.data == inputNumber
- Check Node (Node B) is non leaf node
- Non leaf node (Node B) has only one child
- Connect Node A to child of Node B (i.e. Node D)
- Connect Node A to Node D.
- Link of Node B is removed from BST
- Delete the Node B
Example 3: Delete node having left & right child nodes from BST
Let us delete Node C from binary search tree.
- Node C has left and right child, so we can not delete the Node C from binary search tree
- Otherwise we will lose underlying nodes.
- We need to reduce Example3 to either Example 1 or Example 2.
Algorithm: remove node having both child nodes from BST using java
- Search the Node C in BST
- Check Node C is non leaf node
- Non Leaf node has both left and right child nodes.
- We need to reduce this case to either example 1 or example 2
- We can not delete Node C directly.
- We will find the minimum element in right subtree
- We found Node J (data is 160) in right subtree
- We will assign the value of Node J to Node C
- Node C will have value equals 160.
- BST have duplicate values (Node C and Node J having 160 value)
- We will delete Node J from BST
- We have reduced it to Example 1 (deleting a leaf node)
- Hence, Node C (Value 150) is deleted from BST.
Program – delete or remove node from binary search tree (BST) using java
We have categorized the code into three sections [Example 1, Example 3 and Example 3], as discussed above.
1.) DeleteNodeInBST Class:
- DeleteNodeInBST delete the node from BST and DeleteNodeInBST has following methods:
- min method, finds the minimum element in the right subtree.
- deleteNodeInBST method, delete a node from binary search tree.
- inorder method will print the binary tree in sorted order.
package org.learn.Question;
import org.learn.PrepareTree.Node;
public class DeleteNodeInBST {
public static void inorder(Node root) {
if (root == null)
return;
inorder(root.left);
System.out.printf("%d ", root.data);
inorder(root.right);
}
private static int min(Node node) {
if (node.left == null) {
return node.data;
}
return min(node.left);
}
public static Node deleteNodeInBST(Node node, int data) {
if (null == node) {
System.out.println("Element is not there in binary search tree");
return null;
}
if (data < node.data) {
node.left = deleteNodeInBST(node.left, data);
} else if (data > node.data) {
node.right = deleteNodeInBST(node.right, data);
} else { // case for equality
// Now we see that whether we can directly delete the node
// [Scenario 3]
if (node.left != null && node.right != null) {
int minInRightSubTree = min(node.right);
node.data = minInRightSubTree;
node.right = deleteNodeInBST(node.right, minInRightSubTree);
} else { // either one child or leaf node
// [Scenario 1 and Scenario 2]
if (node.left == null && node.right == null) {
node = null;
} else {// one child case
Node deleteNode = node;
node = (node.left != null) ? (node.left) : (node.right);
deleteNode = null;
}
}
}
return node;
}
}
2.) Node Class:
- Node class representing the node of binary tree.
package org.learn.PrepareTree;
public class Node {
public int data;
public Node left;
public Node right;
public Node(int num) {
this.data = num;
this.left = null;
this.right = null;
}
public Node() {
this.left = null;
this.right = null;
}
public static Node createNode(int number) {
return new Node(number);
}
}
3.) App Class:
- We are creating the binary tree in main method.
- We are deleting a node from binary search tree.
- We are printing the BST using InOrder binary tree traversal.
package org.learn.Client;
import org.learn.PrepareTree.Node;
import org.learn.Question.DeleteNodeInBST;
public class App
{
public static void main( String[] args )
{
//root level 0
Node A = Node.createNode(100);
//Level 1
Node B = Node.createNode(50);
Node C = Node.createNode(150);
//Level 2
Node D = Node.createNode(25);
Node E = Node.createNode(75);
Node F = Node.createNode(125);
Node G = Node.createNode(175);
//Level 3
Node H = Node.createNode(120);
Node I = Node.createNode(140);
Node J = Node.createNode(160);
Node K = Node.createNode(190);
//connect Level 0 and 1
A.left = B;
A.right = C;
//connect level 1 and level 2
B.left = D;
B.right = E;
C.left = F;
C.right = G;
//Connect level 2 and level 3
F.left = H;
F.right = I;
G.left = J;
G.right = K;
System.out.printf("Deleting %d from binary search tree\n",H.data);
DeleteNodeInBST.deleteNodeInBST(A, H.data);
System.out.println("Binary Tree after deleting node");
DeleteNodeInBST.inorder(A);
System.out.printf("\n\nDeleting %d from binary search tree\n",E.data);
DeleteNodeInBST.deleteNodeInBST(A, E.data);
System.out.println("Binary Tree after deleting node");
DeleteNodeInBST.inorder(A);
System.out.printf("\n\nDeleting %d from binary search tree\n",F.data);
DeleteNodeInBST.deleteNodeInBST(A, F.data);
System.out.println("Binary Tree after deleting node");
DeleteNodeInBST.inorder(A);
System.out.printf("\n\nDeleting %d from binary search tree\n",C.data);
DeleteNodeInBST.deleteNodeInBST(A, C.data);
System.out.println("Binary Tree after deleting node");
DeleteNodeInBST.inorder(A);
}
}
Output – delete or remove node from binary search tree (BST) using java
Deleting 120 from binary search tree Binary Tree after deleting node 25 50 75 100 125 140 150 160 175 190 Deleting 75 from binary search tree Binary Tree after deleting node 25 50 100 125 140 150 160 175 190 Deleting 125 from binary search tree Binary Tree after deleting node 25 50 100 140 150 160 175 190 Deleting 150 from binary search tree Binary Tree after deleting node 25 50 100 140 160 175 190
