Check given binary tree is binary search tree (java/ recursive/ examples)

Given a binary tree, check whether given binary tree is binary search tree or not.
- Traverse the binary tree using depth first search (DFS) recursive algorithm.
What is binary search tree (bst) ?
- Left child of binary tree is less than its parent node
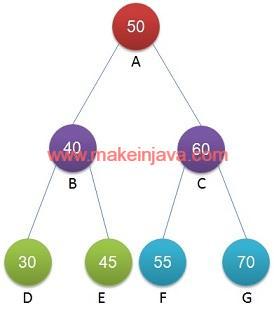
  - e.g. Node B is less than Node A (Fig 1).
- Right child of binary tree is greater than its parent node.
  - e.g. Node C is greater than Node A (Fig 1).
- Binary Tree will be binary search tree, if above properties holds good for every node in a binary tree.

check binary search tree — Fig 1: Check binary tree is BST

Algorithm: check given binary tree is binary search tree in java

Node A is root of binary tree.
Node B is less than Node A
- Check left & right child of node B
  - Node D is less than Node B
  - Node E is greater than Node E
Node C is greater the Node A
- Similarly verify the properties with children of Node C.
Above algorithm should suffice to check whether binary tree is BST.

Optimized algorithm to check given binary tree is binary search tree

At every non leaf node, check the possible value ranges
Node A can have value ranging from Integer.MIN_VALUE to Integer.Max_Value
- So, there is no restriction of value for root node of BST.
What are the possible values of Node B?
- Node B is left child of Root A
- Node B can have any value that is less than A (i.e. <50)
What are the possible values of Node C?
- Node C is right child of Root A
- Node C can have any value that is greater than A (i.e. >50)
What will be possible value for Node F?
- As F is left child Node C and it can have value less than Node C (i.e. <60)
- Can we know what is minimum it can have?
- Yes, It can hold all values greater than Node A and less than Node C
  - Node F > Node A & Node F < Node C
What will be possible value range for Node E?
- Similar to Node F, Its range will be:Node E > Node B and Node E < Node A

Examples: check binary tree is binary search tree using recursive algorithm

Example 1: Check given binary tree is binary search tree

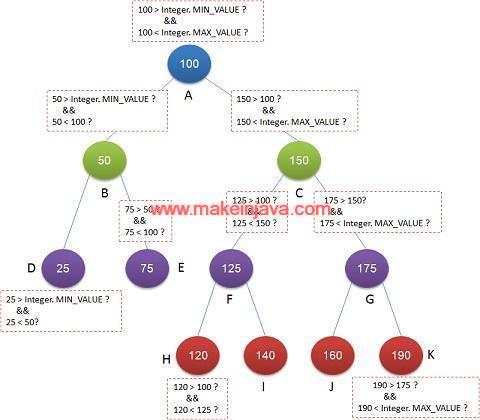
range value node BST — Fig 2: Value at every non leaf node

The above binary tree is binary search tree, as every node within its specified range.

Example 2: Given binary tree is not binary search tree.

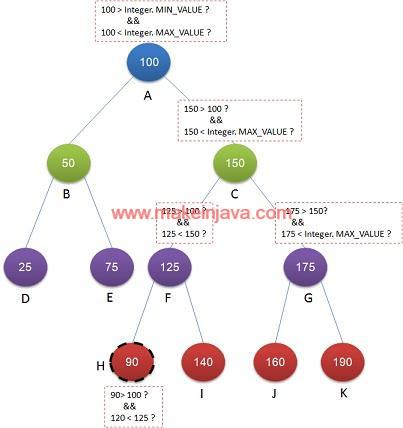
We have modified value Node H of Fig 2. We changed it to 90.
We can see that Node H is less than Node F.
- It should be greater than Node A value (as it on right side A).
Its violation of BST properties.
Binary tree is not a BST.

Time Complexity of algorithm is O(n).

Program – Check given binary tree is binary search tree in java

1.) IsBST Class:

IsBST class check whether given binary tree is binary search tree or not.
Traverse the binary tree using recursive algorithm.

package org.learn.Question;
 
import org.learn.PrepareTree.Node;
 
public class IsBST {
    public static boolean isBST(Node node) {
        return IsBST.isBST(node, Integer.MIN_VALUE, Integer.MAX_VALUE);
    }
 
    private static boolean isBST(Node node, int min, int max) {
        if (node == null)
            return true;
 
        if (node.data < min || node.data > max)
            return false;
 
        boolean isLeft = isBST(node.left, min, node.data);
        if (!isLeft)
            return isLeft;
 
        boolean isRight = isBST(node.right, node.data, max);
        if (!isRight)
            return isRight;
 
        return true;
    }
}

2.) Node Class:

Node class representing the node of a binary tree.

package org.learn.PrepareTree;
 
public class Node {
    public int data;
    public Node left;
    public Node right;
 
    public Node(int num) {
        this.data = num;
        this.left = null;
        this.right = null;
    }
 
    public Node() {
        this.left = null;
        this.right = null;
    }
    public static Node createNode(int number) {
        return new Node(number);
    }
}

3.) App class:

We are creating binary tree in a main method.
We are calling method of IsBST class, to check given binary tree is binary search tree (or not).

package org.learn.Client;
 
import org.learn.PrepareTree.Node;
import org.learn.Question.IsBST;
 
public class App 
{
    public static void main( String[] args )
    {  
       //root level 0
       Node A = Node.createNode(100);
       //Level 1
       Node B = Node.createNode(50);
       Node C = Node.createNode(150);
       //Level 2
       Node D = Node.createNode(25);
       Node E = Node.createNode(75);
       Node F = Node.createNode(125);
       Node G = Node.createNode(175);
       //Level 3
       Node H = Node.createNode(120);
       Node I = Node.createNode(140);
       Node J = Node.createNode(160);
       Node K = Node.createNode(190);
              
       //connect Level 0 and 1
       A.left  = B;
       A.right = C;
       //connect level 1 and level 2
       B.left  = D;
       B.right = E;
       C.left  = F;
       C.right = G;
       //Connect level 2 and level 3
       F.left  = H;
       F.right = I;
       G.left  = J;
       G.right = K;
          
       if(IsBST.isBST(A)) {
           System.out.println("Binary Tree is binary search tree");;
       } else {
           System.out.println("Binary Tree is not binary search tree");
       }
        
       Node H1 = Node.createNode(90);
       F.left  = H1;
       if(IsBST.isBST(A)) {
           System.out.println("Binary Tree is binary search tree");;
       } else {
           System.out.println("Binary Tree is not binary search tree");
       }
    }
}

Output – check given binary tree is BST in java (Fig 2 & Fig 3)

Binary Tree is binary search tree
Binary Tree is not binary search tree

Algorithm: check given binary tree is binary search tree in java

Optimized algorithm to check given binary tree is binary search tree

Examples: check binary tree is binary search tree using recursive algorithm

Example 1: Check given binary tree is binary search tree

Example 2: Given binary tree is not binary search tree.

Program – Check given binary tree is binary search tree in java

1.) IsBST Class:

2.) Node Class:

3.) App class:

Output – check given binary tree is BST in java (Fig 2 & Fig 3)

You may also like: