- Given two binary trees, find out one binary tree is Quasi Isomorphic of other binary tree.
- Traverse the binary tree using depth first search (DFS) recursive algorithm.
- What is Quasi Isomorphic tree?
- Trees having identical structure or obtained by swapping (or mirror binary tree) its children are called Quasi isomorphic trees.
- In quasi isomorphic trees, we are concerned about structures only (we will not consider data of nodes).
- Tree will be quasi isomorphic if any subtree satisfies either of following conditions.
- Identical binary tree: Structure of one subtree tree is identical to another subtree.
- Mirror binary tree: Structure of one subtree is mirror of another subtree.
- We have already discussed similar problem Check whether binary trees are Isomorphic.
Example – Quasi-isomorphic binary trees in java.
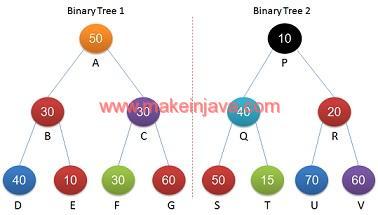
Example 1: Given two Identical binary trees in java (Fig 1).
- Tree shown in Fig 1 have identical structure.
- Ignore the data of respective nodes.
- Binary trees are quasi-isomorphic.
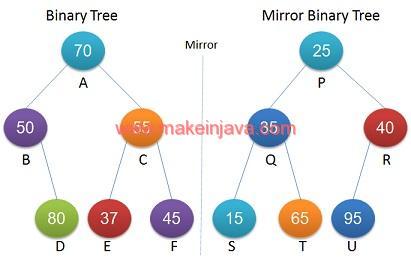
Example 2: Binary tree & mirror binary trees in java.
- One tree is mirror of another binary tree shown in Fig 2.
- Ignore the data of respective nodes.
- Binary trees are quasi-isomorphic.
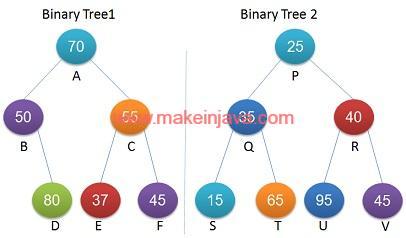
Example 3: One binary tree is not quasi-isomorphic of other binary tree.
- One tree (or subtree) is neither identical nor mirror to another binary tree.
- Trees are not quasi-isomorphic.
Example 4: Quasi-Isomorphic binary trees are shown (Fig 4)
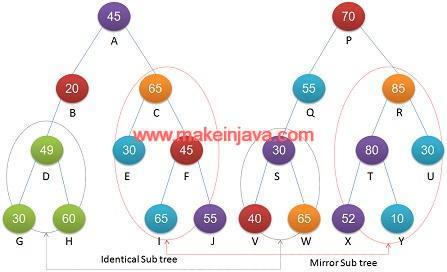
- Nodes A, B, C & Nodes P,Q,R of tree1 & tree2 are identical subtree trees.
- Nodes D, G, H & Nodes S,V,W of tree1 & tree2 are identical subtree trees.
- Nodes C, E, F, I ,J & Nodes R,T,U,X,Y of tree1 & tree2 are mirror subtree of binary trees.
- Both trees are quasi-isomorphic.
Algorithm: check whether binary trees are quasi isomorphic (recursive).
- Evaluate the Current Nodes of tree1 & tree2
- If any of the tree is null
- Trees are not quasi isomorphic & return false
- Check both trees tree1 and tree2
- if tree1 and tree2 are null, traversal completed successfully.
- return true
- Let us check if trees are identical binary trees
- Traverse Left subtree of tree1 and left subtree of tree2
- Traverse Right subtree of tree1 and right subtree of tree2
- If structures are identical, then return true
- If trees are not identical, let us check one tree (or subtree) are mirror of other tree (subtree)
- Traverse Left subtree of tree1 and right subtree of tree2
- Traverse Right subtree of tree1 and left subtree of tree2
- If structures are mirror structure, then return true
- Else, return false
- At the end of traversal, we will know whether trees are quasi isomorphic
Program – check binary trees are quasi isomorphic (recursive algorithm)
1.) QuasiIsomorphicBinaryTree :
- QuasiIsomorphicBinaryTree class is responsible for checking that binary trees are Quasi Isomorphic.
package org.learn.Question;public class QuasiIsomorphicBinaryTree { public static boolean quasiIsomorphicBinaryTree(Node tree1, Node tree2) { if(tree1 == null && tree2 == null) { return true; } if(tree1 == null || tree2 == null) { return false; } //Check identical case if(quasiIsomorphicBinaryTree(tree1.left,tree2.left) && quasiIsomorphicBinaryTree(tree1.right,tree2.right)) return true; //Check mirror case if(quasiIsomorphicBinaryTree(tree1.left,tree2.right) && quasiIsomorphicBinaryTree(tree1.right,tree2.left)) return true; return false; }} |
2.) App Class:
- We are constructing binary trees in main method
- We are invoking quasiIsomorphicBinaryTree method to check whether trees are quasi isomorphic.
package org.learn.Client;import org.learn.Question.Node;import org.learn.Question.QuasiIsomorphicBinaryTree;public class App { public static void main( String[] args ) { //level 0 Node tree1 = Node.createNode(45); //A //level 1 tree1.left = Node.createNode(20); //B tree1.right = Node.createNode(65);//C // left sub tree tree1.left.left = Node.createNode(49);//D tree1.left.left.left = Node.createNode(30);//G tree1.left.left.right = Node.createNode(45); //H // right subtree tree1.right.left = Node.createNode(30); //E tree1.right.right = Node.createNode(60);//F tree1.right.right.left = Node.createNode(65);//I tree1.right.right.right = Node.createNode(55);//J Node tree2 = Node.createNode(70); //P //level 1 tree2.left = Node.createNode(55); //Q tree2.right = Node.createNode(85);//R // left sub tree tree2.left.left = Node.createNode(30);//S tree2.left.left.left = Node.createNode(80);//T tree2.left.left.right = Node.createNode(30); //U // right subtree tree2.right.left = Node.createNode(40); //V tree2.right.right = Node.createNode(65); //W tree2.right.left.left = Node.createNode(52); //X tree2.right.left.right = Node.createNode(10); //Y boolean isSame = QuasiIsomorphicBinaryTree.quasiIsomorphicBinaryTree(tree1, tree2); if(isSame) { System.out.println("Binary trees are Quasi-Isomorphic"); } else { System.out.println("Binary trees are not Quasi-Isomorphic"); } }} |
3.) Node class :
- Node class representing the nodes of binary tree.
package org.learn.Question;public class Node { public int data; public Node left; public Node right; public Node(int num) { this.data = num; this.left = null; this.right = null; } public Node() { this.left = null; this.right = null; } public static Node createNode(int number) { return new Node(number); }} |
Output – check binary trees are quasi isomorphic in java
Binary trees are Quasi-Isomorphic |
Download Code – Quasi-Isomorphic binary trees (recursive algorithm)
