- Given a binary search tree (BST), find the ceil value of input key using recursive algorithm.
- Traverse the binary search tree using depth first search algorithm.
- What is Ceil value in BST?
- The smallest value just greater than or equal to given input key or data.
- We have already discussed Find floor of input data in BST using DFS.
Let us find the ceil value in a binary search tree (BST), shown in Fig 1.
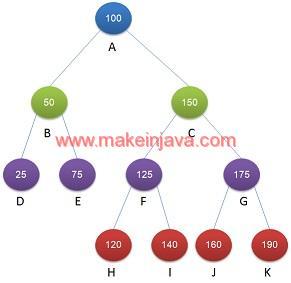
The inorder traversal of binary search tree as shown in Fig 1 is
25 50 75 100 120 125 140 150 160 175 190
Examples – find ceil value of input data in a binary search tree using java
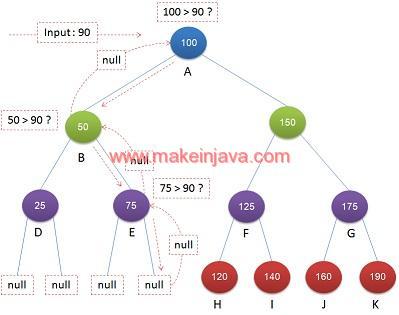
Example 1: find ceil value of input 90 in a given BST (Fig 2).
- Traverse the binary tree using depth first search algorithm.
- At node A, check 100 > 90 ? Ceil value may in left subtree.
- At node B, check 50> 90 ? traverse right subtree.
- At node E, check 75 > 90 ?, traverse right subtree.
- Node E is a leaf node, return null to Node B.
- At node E, check 75 > 90 ?, traverse right subtree.
- return null to Node A.
- At node B, check 50> 90 ? traverse right subtree.
- Node A got null from left subtree, Node A (100) is ceil value for input 90.
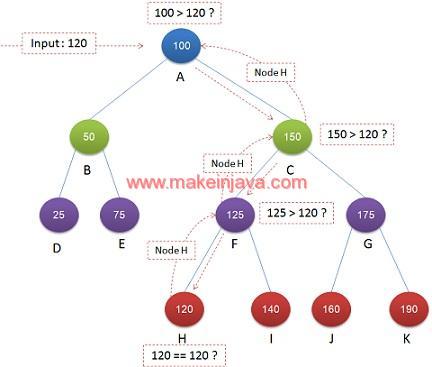
Example 2: calculate ceil value of input 120 in BST (Fig 3).
- At node A, check 100 > 120 ? Ceil value is in right subtree.
- At node C, check 150> 120 ? traverse left subtree.
- At node F, check 125 > 120 ?, traverse left subtree.
- At node H, check 120 == 120 ?, return Node H from here.
- return Node H to Node C.
- At node F, check 125 > 120 ?, traverse left subtree.
- return Node H to Node A.
- At node C, check 150> 120 ? traverse left subtree.
- Node A got non null value i.e. Node H from right subtree, Node H (120) is ceil value for 120.
Example 3: find ceil value of input 126 in a BST (Fig 3).
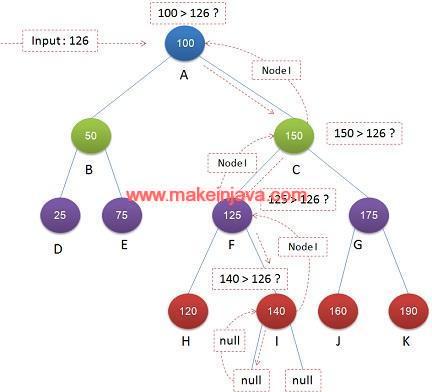
We can analyse the Fig 4 like example 1 & example 2.
Let us summarize to find ceil values of sample input data in a given BST as follows:
| S. No. | Input data | Ceil value |
|---|---|---|
| 1 | 90 | 100 |
| 2 | 120 | 120 |
| 3 | 126 | 140 |
| 4 | 170 | 175 |
Algorithm: find ceil value in a BST (recursive/DFS) using java
- Traverse the binary search tree to find ceil value
- Method is: ceilInBST(Node root, int data)
- If data of current node equals input data
- Then current node is Ceil node for input data
- return the current node from here
- If data of current node is greater the input data
- Traverse the left sub tree to find smaller values.
- If found value in left sub tree
- return the node got from left sub tree
- Else, return the current node
- If we are here, we will find the Ceil value in right subtree
- Traverse the right subtree, to find out Ceil value
- return node from right subtree
- Traverse the right subtree, to find out Ceil value
- By the end of traversal, we will get the Ceil value in a BST.
Time complexity of algorithm: O(log(n))
Calculate ceil value of input data in a binary search tree (DFS) using java
1.) CeilInBST Class:
- CeilInBST class is responsible for finding the ceil value in a BST using recursive algorithm.
package org.learn.Question;
import org.learn.PrepareTree.Node;
public class CeilInBST {
public static Node ceilInBST(Node root, int data) {
if (root == null)
return root;
if (root.data == data)
return root;
if (root.data > data) {
Node left = ceilInBST(root.left, data);
if (left == null)
return root;
else
return left;
}
return ceilInBST(root.right, data);
}
public static void inorder(Node root) {
if(root == null)
return;
inorder(root.left);
System.out.printf("%d ",root.data);
inorder(root.right);
}
}
2.) Node Class:
Node class is representing the nodes of binary tree. Node class has following attributes
- Data Node
- left child
- right child
package org.learn.PrepareTree;
public class Node {
public int data;
public Node left;
public Node right;
public Node(int num) {
this.data = num;
this.left = null;
this.right = null;
}
public Node() {
this.left = null;
this.right = null;
}
public static Node createNode(int number) {
return new Node(number);
}
}
3.) App Class :
- We are creating the binary search tree in a main method.
- We are calling the methods of CeilInBST class, to find ceil value in a BST using recursive algorithm.
package org.learn.Client;
import org.learn.PrepareTree.Node;
import org.learn.Question.CeilInBST;
public class App
{
public static void main( String[] args )
{
//root level 0
Node A = Node.createNode(100);
//Level 1
Node B = Node.createNode(50);
Node C = Node.createNode(150);
//Level 2
Node D = Node.createNode(25);
Node E = Node.createNode(75);
Node F = Node.createNode(125);
Node G = Node.createNode(175);
//Level 3
Node H = Node.createNode(120);
Node I = Node.createNode(140);
Node J = Node.createNode(160);
Node K = Node.createNode(190);
//connect Level 0 and 1
A.left = B;
A.right = C;
//connect level 1 and level 2
B.left = D;
B.right = E;
C.left = F;
C.right = G;
//Connect level 2 and level 3
F.left = H;
F.right = I;
G.left = J;
G.right = K;
System.out.println("Inorder Traversal of BST");
CeilInBST.inorder(A);
int data = 90;
Node floor = CeilInBST.ceilInBST(A, data);
if(null != floor) {
System.out.printf("\nCeil value of %d is %d",data,floor.data);
}
data = 120;
floor = CeilInBST.ceilInBST(A, data);
if(null != floor) {
System.out.printf("\nCeil value of %d is %d",data,floor.data);
}
data = 126;
floor = CeilInBST.ceilInBST(A, data);
if(null != floor) {
System.out.printf("\nCeil value of %d is %d",data,floor.data);
}
data = 170;
floor = CeilInBST.ceilInBST(A, data);
if(null != floor) {
System.out.printf("\nCeil value of %d is %d",data,floor.data);
}
}
}
Output – ceil value of input key in a binary search tree (DFS)
Inorder Traversal of BST 25 50 75 100 120 125 140 150 160 175 190 Ceil value of 90 is 100 Ceil value of 120 is 120 Ceil value of 126 is 140 Ceil value of 170 is 175
Download Code – Ceil value in BST (DFS / recursive algorithm)
