Print binary search tree for given range K1 & K2 in java (DFS & example)

• Given a binary search tree, Print keys of BST in a given input range k1 & k2.
  • We will use depth first search DFS recursive binary tree traversal algorithm.
• Suppose, We are given input range of K1 and K2.
  • Print all keys of BST in range of K1 and k2 i.e. key >= k1 & key <= k2)

Example – print binary search tree for given range K1 & K2 in java

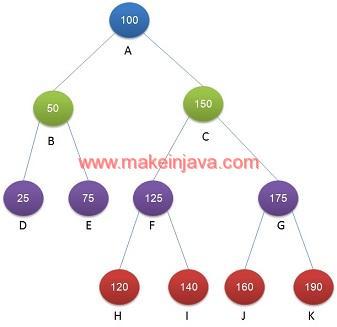
• Suppose input range is K1 = 10 and K2 = 60 for BST
  • We should get the output keys: 25 50
• If input range is K1 = 50 and K2 = 125 for BST
  • We should get the output keys: 100 50 75 125 120
• At every node, we print the keys which are within input range of K1 and K2.

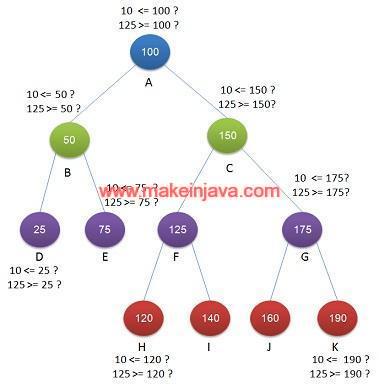
Algorithm – print binary search tree  in range K1=10 & K2=125 using java

In Fig 2, we have shown evaluation condition on few nodes.

• Pre order tree traversal, starting from A node (root)
• Check the current node within range of K1 and K2
  • root.data >= 10 && root.data <= 125 ?
    • if yes, print the data
• Traverse to left sub tree
  • Traverse to left subtree if current node is greater than 10
  • root.data > 10 ?
    • if yes, go to left sub tree
• Traverse to right sub tree
  • Traverse to right sub tree if current node is less than 125
  • root.data < 125 ?
    • if yes, go to right sub tree
• At last, we will able to print the data of binary tree, in given range of K1 and K2
• Time Complexity : O(n)

Program – Print binary search tree (BST) in range of K1 & K2 using java

1.) PrintInRangeBST Class:

• Perform the pre order traversal of BST
• Print the BST in a given range (K1 and K2)

package org.learn.Question;

import org.learn.PrepareTree.Node;

public class PrintInRangeBST {
 public static void printRange(Node root, int k1, int k2) {
  if (root == null)
   return;
  if (root.data >= k1 && root.data <= k2)
   System.out.printf("%d ", root.data);
  if (root.data > k1)
   printRange(root.left, k1, k2);
  if (root.data < k2)
   printRange(root.right, k1, k2);
 }
}

2.) Node Class:

• Node class representing the node of a binary search tree.

package org.learn.PrepareTree;

public class Node {
 public int data;
 public Node left;
 public Node right;

 public Node(int num) {
  this.data = num;
  this.left = null;
  this.right = null;
 }

 public Node() {
  this.left = null;
  this.right = null;
 }
 public static Node createNode(int number) {
  return new Node(number);
 }
}

3.) App Class:

• We are creating the binary search tree in main method.
• We are calling PrintInRangeBST class, to print the binary search tree within a range (K1 and K2) using DFS recursive algorithm.

package org.learn.Client;

import org.learn.PrepareTree.Node;
import org.learn.Question.PrintInRangeBST;

public class App 
{
    public static void main( String[] args )
    {  
       //root level 0
       Node A = Node.createNode(100);
       //Level 1
       Node B = Node.createNode(50);
       Node C = Node.createNode(150);
       //Level 2
       Node D = Node.createNode(25);
       Node E = Node.createNode(75);
       Node F = Node.createNode(125);
       Node G = Node.createNode(175);
       //Level 3
       Node H = Node.createNode(120);
       Node I = Node.createNode(140);
       Node J = Node.createNode(160);
       Node K = Node.createNode(190);
             
       //connect Level 0 and 1
       A.left = B;
       A.right = C;
       //connect level 1 and level 2
       B.left = D;
       B.right = E;
       C.left = F;
       C.right = G;
       //Connect level 2 and level 3
       F.left = H;
       F.right = I;
       G.left = J;
       G.right = K;
       
       int K1 = 10;
       int K2 = 125;
       System.out.printf("Printing binary tree in range %d and %d\n",K1, K2);
       PrintInRangeBST.printRange(A, K1, K2);     
    }
}

Output – print binary search tree (BST) in range of K1 & K2 using java

Printing binary tree in range 10 and 125
100 50 25 75 125 120

Download Code – print binary search tree in range K1 & K2 (DFS)